DDPM

Stable Diffusion

　　　　

VAE

Maximum Likelihood

VAE(Variational Autoencoders) 는 latent variable $z$로 개별 데이터를 생성할 수 있는 Generative Model이다. MLE(Maximum Likelihood Estimation)관점에서의 모델의 학습에 대해 먼저 설명하면 input $z$와 target $x$가 있을 때, $f_{\theta}(\cdot)$ 는 모델(가우시안, 베르누이.. )이고, 최종 목표는 target이 나올 확률인 $p(x | f_{\theta}(z))$가 최대가 되도록 하는 $\theta$를 찾는 것이다. MLE에서는 학습전에 학습할 확률분포(가우시안, 베르누이.. )를 먼저 정하고, 모델의 출력은 이 확률 분포를 정하기 위한 파라미터(가우시안의 경우 $\mu, \sigma^2$)라고 해석할 수 있다. 결과적으로 target을 잘 생성하는 모델 파라미터 $\theta$는 $\theta^* = \underset{\theta}{\arg\min} [-\log(p(x \vert f_{\theta}(z)))]$가 된다. 이렇게 찾은 $\theta^*$는 확률분포를 찾은 것이므로 결과에 대한 sampling이 가능하고, 이 sampling에 따라 다양한 이미지가 생성될 수 있는 것이다.

VAE의 Decoder도 위와 비슷하다. Encoder 부분은 regularizer로, variational inference approximate posterior $q(z \vert x)$를 prior $p(z)$에 근사시키는 것과 관련되며, Decoder 부분은 latent variable $z$를 입력으로 받아 encoder의 입력값으로 주어진 데이터와 비교해 reconstruction error를 줄이는 방향으로 업데이트 된다. 이때 $z$는 controller로서 생성될 이미지를 조정하는 역할을 할 수 있다. 예를 들면 고양이의 귀여움을 조정하여 더 귀여운 고양이 이미지를 생성하는 것이다.

다시 돌아와서 결과적으로 VAE의 목적은 모든 training data $x$에 대해 $x$가 나올 확률 $p(x)$를 구하는 것이 목적이다. 이때 training data에 있는 sample과 유사한 sample을 생성하기 위해서 prior 값을 이용하는데, 이 값이 Latent Variable인 $z$가 나올 확률 $p(z)$이고, $p(x)$ 는 $\int p(x \vert g_{\theta}(z))p(z)dz=p(x)$로 구해진다. MLE(Maximum Likelihood Estimation) 와 MAP(Maximum A Posteriori) 에 대한 자세한 내용은 reference에 있다.

Prior Distribution

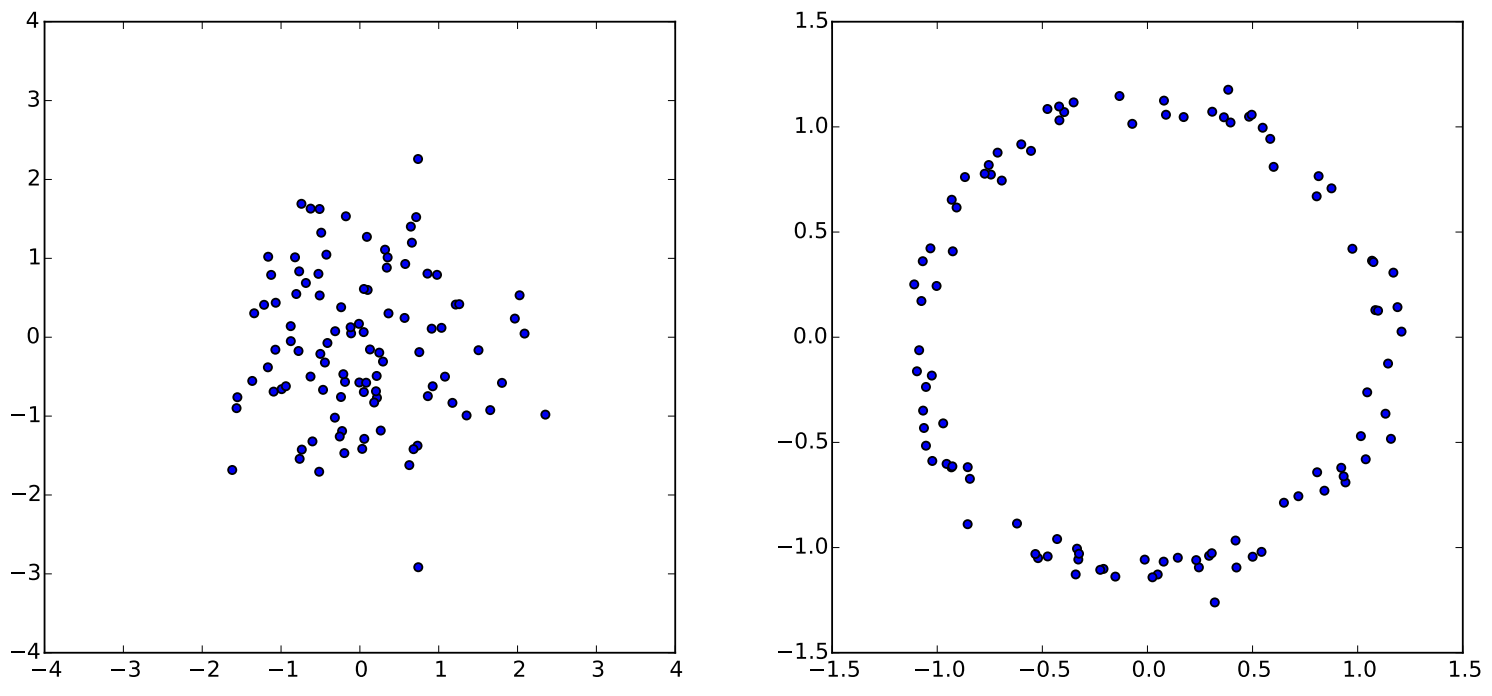
앞서 말했듯이 $z$는 controller 역할을 하기 때문에 $z$를 잘 조정할 수 있어야 한다. 이때 $z$는 고차원 input에 대한 manifold 상에서의 값들인데, generator의 input으로 들어가기 위해 sampling된 값이 이 manifold 공간을 잘 대표하는가? 라는 질문이 나온다. 위 사진을 보면 왼쪽에 normally-distributed 된 분포가 있을 때 해당 분포에

\[g(z) = \frac{z}{10} + \frac{z}{ \parallel z \parallel}\]

를 적용하면 오른쪽 처럼 ring 형태의 분포가 나오는 것을 확인할 수 있다. 이처럼 간단한 변형으로 manifold를 대표할 수 있기 때문에 모델이 DNN 이라면, 학습해야 하는 manifold가 복잡하다 하더라도, DNN의 한 두개의 layer가 manifold를 찾기위한 역할로 사용될 수 있다. 따라서 Prior Distribution을 normal distribution과 같은 간단한 distribution으로 해도 상관없다.

Variational Inference

$p(x \vert g_{\theta}(z))$의 likelihood가 최대가 되는 것이 목표라면 Maximum Likelihood Estimation를 직접적으로 사용해서 구하면 될거 같은데 실제론 그렇지 않다. 그 이유는 가우시안 분포라 가정했을 때, $p(x \vert g_{\theta}(z))$의 log loss인 $-\log(p(x \vert g_{\theta}(z)))$는 Mean Squared Error와 같아진다. 즉, MSE의 관점에서 loss가 작은 것이 $p(x)$에 더 크게 관여하는데, MSE loss가 작은 이미지가 실제 의미적으로 더 가까운 이미지가 아닌 경우가 많기 때문에 올바른 방향으로 학습할 수가 없다.

\[{\parallel x - z_{bad} \parallel}^2 < {\parallel x - z_{good} \parallel}^2 \to p(x \vert g_{\theta}(z_{bad})) > p(x \vert g_{\theta}(z_{good}))\]

예를 들면 원래 고양이 이미지에서 일부분이 조금 잘린 이미지 $a$와 한 pixel씩 옆으로 이동한 이미지 $b$가 있다고 하면 $b$는 pixel만 옆으로 밀렸을 뿐 고양이 그대로 이지만 $a$는 이미지가 잘렸기 때문에 의미적으론 $b$가 $a$보다 고양이에 가까운데, MSE 관점에서는 $b$의 loss가 더 크게 나오게 된다.

이러한 문제를 해결하기 위해 Variational Inference가 나오게 된다. 기존 prior에서 sampling을 하니 학습이 잘 안되니까 $z$ 를 prior에서 sampling하지 말고 target인 $x$ 와 유사한 sample이 나올 수 있는 이상적인 확률분포 $p(z \vert x)$ 로 부터 sampling한다. 이때 우리는 $p(z \vert x)$ 가 무엇인지 알지 못하기 때문에, 이미 알고 있는 확률 분포(가우시안..) $q_{\phi}(z \vert x)$ 를 임의로 택하고 그것의 파라미터 $\phi$ 를 조정하여 $p(z \vert x)$ 와 유사하게 되도록 하는 것이다. 그렇게 이상적인 확률분포에 근사된 $q_{\phi}$ 를 통해서 $z$ 를 sampling하게 된다.

\[p(z \vert x) \approx q_{\phi}(z \vert x) \sim z\]

ELBO

지금까지의 내용을 정리하면 우리가 구하고자 하는 것은 $p(x)$였고, 이를 위해 Prior Distribution을 사용했으며, 그냥 prior에서 sampling하려니 잘 학습이 안되서 이상적인 확률분포 $p(z|x)$ 를 근사한 $q_{\phi}$를 사용하게 됐다. 이 4개간의 관계식에서 loss를 유도하는 과정에 우리가 찾아야 하는 ELBO(Evidence LowerBOund)가 나오게 된다.

우선 $\log(p(x))$에서 시작해서 ELBO를 유도하는 과정을 정리하면 아래와 같다.

\[\begin{aligned} \log(p(x)) &= \int \log(p(x))q_{\phi}(z|x)dz 　 \leftarrow \int q_{\phi}(z|x)dz = 1 \\ &=\int \log\left(\frac{p(x, z)}{p(z|x)}\right)q_{\phi}(z|x)dz 　 \leftarrow p(x) = \frac{p(x, z)}{p(z|x)} \\ &=\int \log\left(\frac{p(x, z)}{q_{\phi}(z|x)}\cdot\frac{q_{\phi}(z|x)}{p(z|x)}\right)q_{\phi}(z|x)dz \\ &=\int \underbrace{\log\left(\frac{p(x, z)}{q_{\phi}(z|x)}\right)q_{\phi}(z|x)dz}_ {ELBO(\phi)} + \int \underbrace{\log\left(\frac{q_{\phi}(z|x)}{p(z|x)}\right)q_{\phi}(z|x)dz}_ {KL\left(q_{\phi}(z|x) \ || \ p(z|x)\right)} \\ \end{aligned}\]

여기서 $KL \left(q_{\phi}(z \vert x) \ \parallel \ p(z \vert x)\right)$ term은 Kullback–Leibler divergence로 두 확률분포 간의 차이($\ge 0$)를 구한다. 우리가 원하는 건 $q_{\phi}(z \vert x)$가 $p(z \vert x)$에 최대한 가까워 져야 하므로 $KL$을 최소화 하는 $q_{\phi}(z \vert x)$의 $\phi$를 찾아야 하는데 $p(z \vert x)$를 모르기 때문에 KL을 최소화 하는 대신 $ELBO$를 최대화 하는 $\phi$를 찾으면 된다.

\[\log(p(x)) = ELBO(\phi) + KL(\left(q_{\phi}(z|x) \ || \ p(z|x)\right)\] \[q_{\phi^*}(z|x) = \underset{\phi}{\arg\max} \ ELBO(\phi)\]

$ELBO$를 최대화 하기 위해 $ELBO$ term을 다시 전개하면 다음과 같다.

\[\begin{aligned} ELBO(\phi) &= \int \log \left(\frac{p(x, z)}{q_{\phi}(z|x)}\right)q_{\phi}(z|x)dz \\ &= \int \log \left(\frac{p(x|z)p(z)}{q_{\phi}(z|x)}\right)q_{\phi}(z|x)dz \\ &= \int \log \left(p(x|z)\right)q_{\phi}(z|x)dz - \int \log \left(\frac{q_{\phi}(z|x)}{p(z)}\right)q_{\phi}(z|x)dz \\ &= \mathbb{E}_ {q_{\phi}(z|x)} \left[\log\left(p(x|z)\right)\right] - KL\left(q_{\phi}(z|x) \ || \ p(z)\right) \end{aligned}\]

그래서 정리하면 $ELBO$를 최대화 하는데 있어서 $\phi$, $\theta$로 총 2개에 대한 Optimization Problem을 해결해야 하고 이는 아래와 같다.

Optimization Problem 1 on $\phi$: Variational Inference

\[\log(p(x)) \ge \mathbb{E}_ {q_{\phi}(z \vert x)} \left[\log\left(p(x \vert z)\right)\right] - KL\left(q_{\phi}(z \vert x) \ \parallel \ p(z)\right) = ELBO(\phi)\]

첫 번째로 $ELBO$를 maximize하는 $\phi$를 찾는데, 이 과정이 이상적인 sampling function을 찾는 것이다.

Optimization Problem 2 on $\theta$: Maximum likelihood

\[-\sum_i \log(p(x_i)) \le -\sum_i \lbrace\mathbb{E}_ {q_{\phi}(z \vert x_i)} \left[\log\left( p \left(x_i \vert g_{\theta}(z)\right)\right)\right] - KL\left(q_{\phi}(z \vert x_i) \ \parallel \ p(z)\right)\rbrace\]

두 번째는 이상적인 sampling function을 찾았으므로 여기서 $z$를 sampling해서 $z$로 부터 target $x$가 나오게 하는 Conditional probability $p(x \vert g_{\theta}(z))$가 최대가 되도록 하는 확률분포를 찾는 것이다.
$\mathbb{E}_ {q_{\phi}(z \vert x_i)} \left[\log\left(p(x_i \vert g_{\theta}(z))\right)\right]$는 $q_{\phi}$에서 sampling한 $z$에 대한 $\log\left(p(x_i \vert g_{\theta}(z))\right)$를 의미한다.

Final Optimization Problem

\[\underset{\phi, \theta}{\arg\min} \sum_i -\mathbb{E}_ {q_{\phi}(z \vert x_i)} \left[\log\left( p \left(x_i \vert g_{\theta}(z)\right)\right)\right] + KL\left(q_{\phi}(z \vert x_i) \ \parallel \ p(z)\right)\]

결국 위 두 Optimization Problem을 종합하는 식이 위와 같고, 이 식이 $ELBO$를 최대화하는 것과 같게 된다.

정리해서 이상적으로 sampling을 해주는 $q_{\phi}(z \vert x)$를 Encoder, Posterior, Inference Network 등으로 부르고, sampling된 $z$로 부터 이미지를 generate 해주는 $g_{\theta}(x \vert z)$를 Decoder, Generator, Generation Network 등으로 부른다.

Loss Function

결과적으로 ELBO를 최대화 하기 위한 Loss는 아래와 같이 표현된다.

\[L_i(\phi, \theta, x_i) = \underbrace{-\mathbb{E}_ {q_{\phi}(z \vert x_i)} \left[\log\left( p \left(x_i \vert g_{\theta}(z)\right)\right)\right]}_ \text{Reconstruction Error} + \underbrace{KL\left(q_{\phi}(z \vert x_i) \ \parallel \ p(z)\right)}_ \text{Regularization}\]

Reconstruction Error term은 앞서 말했던 MSE(가우시안의 경우)로 계산되는 부분이다. 해당 term을 결론적으로 보면 $x$를 넣었을 때 $x$가 나올 확률에 대한 것이기 때문에 Reconstruction Error라고 한다. 만약 가정을 베르누이 분포라고 하면 MSE가 아닌 Cross Entropy가 된다.

Regularization는 같은 Reconstruction Error를 갖는 $q_{\phi}$가 여럿 있다면, 그 중에서도 prior $p(z)$와 가까운 $q_{\phi}$를 고르라는 것으로, 생성 데이터에 대한 통제 조건을 prior에 부여하고, 이와 유사해야 한다는 조건을 부여한 것이다.

그럼 이제 $ELBO$를 실제 어떻게 계산하는지 알아보기 전에 $q_{\phi}$를 gaussian distribution $q_{\phi} \sim N(\mu_i, \sigma_i^2I)$, $p(z)$를 normal distribution $p(z) \sim N(0, 1)$으로 가정한다고 하자.

우선 Regularization term의 경우 2개의 가우시안 분포 간의 KL divergence는 아래와 같이 계산된다고 수학적으로 알려져있다.

\[D_{KL}(\mathcal{N}_0 \ \parallel \ \mathcal{N}_1) = \frac{1}{2}\left[ tr\left({Σ_1}^{-1}Σ_0\right) + (\mu_1 - \mu_0)^T {Σ_1}^{-1}(\mu_1 - \mu_0) - k + \ln\frac{\vert Σ_1 \vert}{\vert Σ_0 \vert}\right]\] \[tr(A) = \sum_{i} A_{ii}\]

이는 KL divergence $D_{KL}(p \parallel q) = \int_x p(x)\log \frac{p(x)}{q(x)}$ 를 구할 때 다변량 정규 분포의 pdf가 아래와 같음을 이용하여 유도된 것으로 자세한 내용은 reference에 있다.

\[p(x) = \frac{1}{(2\pi)^{k/2} \vert Σ \vert^{1/2}} \exp \left(- \frac{1}{2} (x-\mu)^{T} {Σ}^{-1} (x - \mu) \right) \\ 　　 Σ = \mathbb{E} \left[ (x - \mu) (x - \mu)^T \right] = \begin{vmatrix} \sigma_{11}^2 & \sigma_{12}^2 & \cdots & \sigma_{1p}^2 \\ \sigma_{21}^2 & \sigma_{22}^2 & \cdots & \sigma_{2p}^2 \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p1}^2 & \sigma_{p2}^2 & \cdots & \sigma_{pp}^2 \end{vmatrix}\]

여기서 $Σ$ 은 공분산 행렬이고, $(x-\mu)^{T} {Σ}^{-1} (x - \mu)$는 마할라노비스 거리(Mahalanobis distance)로 $x$가 평균값 $\mu$에서 얼마나 많은 표준 편차만큼 떨어져 있는가를 나타낸다.

이에 따라 앞서 가정한 $q_{\phi} \sim N(\mu_i, \sigma_i^2I)$, $p(z) \sim N(0, 1)$ 대로 KL term을 계산하면 아래와 같이 된다.

\[\begin{aligned} KL\left(q_{\phi}(z \vert x_i) \ \parallel \ p(z)\right) &= \frac{1}{2} \left\lbrace tr(\sigma_i^2I) + \mu_i^T\mu_i - J + \ln \frac{1}{\prod \sigma_{i,j}^2} \right\rbrace \\ &= \frac{1}{2} \left\lbrace \sum_{j=1}^J \sigma_{i,j}^2 + \sum_{j=1}^J \mu_{i,j}^2 - J - \sum_{j=1}^J \ln(\sigma_{i,j}^2) \right\rbrace \\ &= \frac{1}{2}\sum_{j=1}^J \left(\mu_{i,j}^2 + \sigma_{i,j}^2 - \ln(\sigma_{i,j}^2) - 1\right) \end{aligned}\]

　　　　　 　　　　 　　　 $J$ : $\text{dimension}$
　　　　　 　　　　　 　　 $\mu, \sigma$ : $q_{\phi} \sim N(\mu_i, \sigma_i^2I)$

Reconstruction Error term의 경우 원래라면 아래처럼 기댓값을 구할 때 적분을 해야하지만, 대신 Monte Carlo method로 $L$개를 sampling하여 구한다.

\[\begin{aligned} \mathbb{E}_ {q_{\phi}(z \vert x_i)} \left[\log\left( p \left(x_i \vert g_{\theta}(z)\right)\right)\right] &= \int \log(p_{\theta}(x_i \vert z))q_{\phi}(z \vert x_i)dz \\ &\approx \frac{1}{L}\sum_{z^{i,l}} \log\left(p_{\theta}(x_i \vert z^{i,l})\right) \end{aligned}\]

이때 문제는 $q_{\phi}$에서 random으로 sampling을 하기 때문에 backpropagation에서의 편미분이 불가능하다는 것이다. 그래서 이를 해결하기 위해 reparameterization trick을 사용하는데, 이는 normal distribution $\mathcal{N}(0,1)$에서 sampling한 $\epsilon$에 대해 아래처럼 표현될 수 있다는 점을 이용하여 backpropagation이 가능하도록 한 것이다.

\[z^{i,l} \sim \mathcal{N}(\mu_i, \sigma_i^2I) 　\to　 z^{i,l} = \mu_i + \sigma_i^2 \odot \epsilon 　　\epsilon \sim \mathcal{N}(0,1)\]

Reconstruction Error를 정리하면 아래와 같고 Monte Carlo에서의 sampling의 경우 $L=1$로 하나만 sampling하는 경우가 많다.

\[\mathbb{E}_ {q_{\phi}(z \vert x_i)} \left[\log\left( p \left(x_i \vert g_{\theta}(z)\right)\right)\right] = \int \log(p_{\theta}(x_i \vert z))q_{\phi}(z \vert x_i)dz \approx \frac{1}{L}\sum_{z^{i,l}} \log\left(p_{\theta}(x_i \vert z^{i,l})\right) \approx \log\left(p_{\theta}(x_i \vert z^i)\right) 　\leftarrow L=1\]

그러면 $\log\left(p_{\theta}(x_i \vert z^i)\right)$의 값만 구하면 되는데, 이미지처리의 경우 $p_{\theta}$를 gaussian대신 bernoulli 분포로 정하고 계산한다. 따라서 bernoulli distribution에 따라 구하면 아래와 같이 Cross Entropy의 형태가 나온다.

\[\begin{aligned} \log\left(p_{\theta}(x_i \vert z^i)\right) &= \log \prod_{j=1}^D p_{\theta}(x_{i,j} \vert z^i) = \sum_{j=1}^D \log p_{\theta}(x_{i,j} \vert z^i)　\leftarrow i.i.d \\ &= \sum_{j=1}^D \log p_{i,j}^{x_{i,j}}(1-p_{i,j})^{1-x_{i,j}}　\leftarrow p_{i,j} \circeq network \ output \\ &= \sum_{j=1}^D x_{i,j} \log p_{i,j} + (1-x_{i,j}) \log (1-p_{i,j})　\leftarrow Cross \ entropy \end{aligned}\]

DDPM

Markov Chain

Markov Chain은 Markov 성질을 갖는 이산시간 확률과정을 의미한다. 여기서 Markov 성질은 특정 상태의 확률($t+1$)이 오직 현재($t$)의 상태에만 의존한다는 것을 의미하고, 이산 확률과정이란 이산적인 시간($0s, 1s, 2s,…$)속에서의 확률적 현상을 의미한다.

\[P(S_{t+1} \vert S_t) = P(S_{t+1} \vert S_1,...,S_t)\]

Diffusion Model

Diffusion Model은 input 이미지에 작은 영역에서의 gaussian distribution noise를 여러 단계 Diffusion 시켜서 forward(Noising)하고, backward에서는 이를 다시 복원하는 noise 제거과정(Denoising)을 학습하여 입력 이미지와 유사한 확률 분포를 가진 결과 이미지를 생성할 수 있도록 하는 모델이다.

Diffusion Model모델은 Denoising과정만 학습하게 되는데, 이유는 Noising과정의 $q(x_t \vert x_{t-1})$의 값은 사전에 정의한 gaussian noise에 따라 계산하면 되지만, Denoising과정의 $q(x_{t-1} \vert x_t)$는 $q(x_t \vert x_{t-1})$로 부터 바로 계산해낼 수 없기 때문이다.
모델이 학습해야 하는 값은 $q(x_{t-1} \vert x_t)$이므로 이를 추종하는 $p_{\theta}$를 상정해 $p_{\theta}(x_{t-1} \vert x_t) \approx q(x_{t-1} \vert x_{t})$가 되도록 하는 것이 목표이다.

Diffusion Process

$x_0$을 input image라 하고 $x_T$를 Noise라고 하는데, $x_t$에서 $t$가 커질 수록 Noise에 가까워지게 된다. 각 단계에서 다음 단계로 noise를 추가할 때의 관계는 아래와 같으며 Markov Process을 따른다.

\[q(x_t \vert x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_tI)　　\to　　q(x_{1:T} \vert x_0) = \prod_ {t=1}^T q(x_ t \vert x_ {t-1})\]

이때 주입되는 gaussian noise의 크기는 사전에 정의되며, $\beta_t$로 표기된다. $\beta_t$가 매우 작을 경우 Noising과정의 $q(x_t|x_{t-1})$가 가우시안이면, Denoising과정의 $q(x_{t-1} \vert x_t)$도 가우시안이라는 것이 이미 증명되었다.
$\beta_t$는 $t$가 커질 수록 값이 커지게 설계되는데, scheduling 방식은 크게 Linear scheduling, Sigmoid scheduling, Quadratic scheduling으로 나뉜다. 이에 따라 $\beta_t$가 커질수록 이전 단계($x_{t-1}$)에서 제거되는 정보는 점점 커지고, 분산($\beta_tI$)역시 커지며 Noise가 증가하게 된다.

Diffusion Process는 VAE와 유사하게 Reparameterization Trick으로 계산된다.

\[q(x_t \vert x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_tI) = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1}　*\epsilon \sim \mathcal{N}(0,1)\]

Diffusion Model은 original data $x_0$를 제외한 $x_1, …, x_T$의 값들을 $x_0$에서 시작한 conditional gaussian에서 가져온 latent variable($x_1=z_1,x_2=z_2,..,x_T=z_T$)로 간주한다. 따라서 Diffusion Process는 conditional gaussian의 joint-distribution으로서, $x_0$를 조건부로한 latent variables($x_{1:T}$)를 생성하는 과정이라 할 수 있다.

\[\begin{aligned} q(x_{0:T}) &= q(x_T \vert x_ {T-1}, x_{T-2}, \cdots, x_0)q(x_ {T-1}, x_{T-2}, \cdots, x_0) \\ &= q(x_T \vert x_{T-1})q(x_{T-1}, x_{T-2}, \cdots, x_0) \\ &= q(x_T \vert x_{T-1})q(x_{T-1} \vert x_{T-2}, x_{T-3}, \cdots, x_0)q(x_{T-2}, x_{T-3}, \cdots, x_0) \\ &= q(x_T \vert x_{T-1})q(x_{T-1} \vert x_{T-2})q(x_{T-2}, x_{T-3}, \cdots, x_0) \\ &　　　　\vdots \\ &= q(x_0) \prod_ {t=1}^T q(x_ t \vert x_ {t-1}) \\ &\therefore q(x_{1:T} \vert x_0) = \prod_ {t=1}^T q(x_ t \vert x_ {t-1}) \end{aligned}\]

Reverse Process

앞서 설명했듯이 $\beta_t$가 매우 작을 경우 Reverse Process 역시 가우시안이 된다. 다만 Diffusion Process는 사전에 정의한 $\beta_t$에 의해 각 단계에서의 모수인 평균과 분포가 정의되었지만, Reverse Process는 이를 알지 못하기 때문에 조건부 가우시안 분포의 모수인 평균과 분산을 학습해야 한다.

\[p_{\theta}(x_{0:T}) = p(x_T)\prod_{t=1}^Tp_{\theta}(x_{t-1} \vert x_t), 　　p_{\theta}(x_{t-1} \vert x_t) = \mathcal{N}\left(x_{t-1}; \mu_{\theta}(x_t,t), \sum_{\theta}(x_t,t)\right)\]

따라서 위 식에서 학습해야하는 대상은 $\mu_{\theta}(x_t,t)$과 $\sum_{\theta}(x_t,t)$로 각 $t$시점의 평균과 분산을 구해야 한다.

\[\begin{aligned} p(x_{0:T}) &= \frac{p(x_T)p(x_0, \cdots ,x_T)}{p(x_T)} \\ &= p(x_T)\frac{p(x_{T-1}, x_T)}{p(x_T)}\frac{p(x_{T-2}, x_{T-1}, x_T)}{p(x_{T-1}, x_T)}\cdots\frac{p(x_0, \cdots ,x_T)}{p(x_1, \cdots ,x_{T})} \\ &= p(x_T)p(x_{T-1} \vert x_T)p(x_{T-2} \vert x_{T-1},x_{T}) \cdots p(x_0 \vert x_1, \cdots ,x_T) \\ &= p(x_T)p(x_{T-1} \vert x_T)p(x_{T-2} \vert x_{T-1}) \cdots p(x_0 \vert x_1) \\ &　　　　\vdots \\ &= p(x_T)\prod_{t=1}^Tp(x_{t-1} \vert x_t) \end{aligned}\]

Diffusion Loss

VAE to Diffusion

\(\begin{aligned} -\log p_{\theta}(x_0) &= \int (-\log p_{\theta}(x_0)) \cdot q(x_T \vert x_0)dx_T　　\because \int q(x_T \vert x_0)dx_T=1 \\ &= \int \left( -\log \frac{p_{\theta}(x_0,x_T)}{p_{\theta}(x_T \vert x_0)} \right) \cdot q(x_T \vert x_0)dx_T 　　\because bayes \ rule \\ &= \int \left( -\log \frac{p_{\theta}(x_0,x_T)}{p_{\theta}(x_T \vert x_0)} \cdot \frac{q(x_T \vert x_0)}{q(x_T \vert x_0)} \right) \cdot q(x_T \vert x_0)dx_T \\ &\le \int \left(-\log \frac{p_{\theta}(x_0,x_T)}{q(x_T \vert x_0)} \right) \cdot q(x_T \vert x_0)dx_T　　\because KL \ divergence > 0, \ ELBO \\ &= \int \left(-\log \frac{p_{\theta}(x_0 \vert x_T) \cdot p_{\theta}(x_T)}{q(x_T \vert x_0)} \right) \cdot q(x_T \vert x_0)dx_T 　　\because bayes \ rule \\ &= \int \left(-\log \frac{p_{\theta}(x_0 \vert x_T)}{q(x_T \vert x_0)} \right) \cdot q(x_T \vert x_0)dx_T + \int \left(-\log p_{\theta}(x_T) \right) \cdot q(x_T \vert x_0)dx_T 　　\because separate \ log \\ &= \mathbb{E}_ {x_T \sim q(x_T \vert x_0)} \left[-\log \frac{p_{\theta}(x_0 \vert x_T)}{q(x_T \vert x_0)} \right] +\mathbb{E}_ {x_T \sim q(x_T \vert x_0)}\left[-\log p_{\theta}(x_T)\right] 　　\because definition \ of \ expectation \end{aligned}\)

Diffusion Loss를 전개해보면 VAE Loss와 유사하지만 5번째 줄에서 차이가 있다. VAE Loss에서는 $ELBO$식의 분모가 $p_{\theta}(x_T)$와 결합하지만, Diffusion Loss에서는 $p_{\theta}(x_0 \vert x_T)$ 와 결합한다.
결과적으로 전개해서 나온 식을 보면 $p_{\theta}(x_0 \vert x_T)$와 $q(x_T \vert x_0)$의 KL divergence가 나오고 이는 noising과정의 $q$로부터 $p_{\theta}$가 denoising process를 할 수 있도록 한다.
4번째 줄은 VAE와 마찬가지로 intractable한 KL divergence term을 제거하고 $ELBO$만 남긴다.

Diffusion Loss

앞서 VAE Loss를 변형하여 $KL(p_{\theta} \ \parallel \ q)$가 유도되도록 한 아이디어를 이용해서 Diffusion Loss를 처음부터 전개하면 다음과 같다.

\[\begin{aligned} \mathbb{E}_ {x_T \sim q(x_T|x_0)} \left[-\log p_{\theta}(x_0)\right] &= \mathbb{E}_ {x_T \sim q(x_T|x_0)} \left[-\log \frac{p_{\theta}(x_0,x_1,x_2,...,x_T)}{p_{\theta}(x_1,x_2,x_3,...,x_T|x_0)}\right] 　　\because bayes \ rule \\ &= \mathbb{E}_ {x_T \sim q(x_T|x_0)} \left[-\log \frac{p_{\theta}(x_0,x_1,x_2,...,x_T)}{p_{\theta}(x_1,x_2,x_3,...,x_T|x_0)}\cdot \frac{q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)}\right] \\ &\le \mathbb{E}_ {x_T \sim q(x_T|x_0)}\left[-\log \frac{p_{\theta}(x_0,x_1,x_2,...,x_T)}{q(x_{1:T}|x_0)}\right] 　　\because KL \ divergence > 0, \ ELBO \\ &= \mathbb{E}_ {x_T \sim q(x_T|x_0)}\left[-\log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}\right] 　　\because Notation \\ &= \mathbb{E}_ {x_T \sim q(x_T|x_0)}\left[-\log \frac{p_{\theta}(x_T)\prod p_{\theta}(x_{t-1}|x_t)}{\prod q(x_t|x_{t-1})}\right] 　　\because Below \ Markov \ chain \ property \\ &= \mathbb{E}_ {x_{1:T} \sim q(x_{1:T}|x_0)}\left[-\log p_{\theta}(x_T) - \sum_{t=1}^T \log \frac{p_{\theta}(x_{t-1}|x_t)}{q(x_t|x_{t-1})}\right] 　　\because separating \ to \ summation \ in \ logarithm \\ &= \mathbb{E}_ {x_{1:T} \sim q(x_{1:T}|x_0)}\left[-\log p_{\theta}(x_T) - \sum_{t=2}^T \log \frac{p_{\theta}(x_{t-1}|x_t)}{q(x_t|x_{t-1})} - \log \frac{p_{\theta}(x_0|x_1)}{q(x_1|x_0)}\right] \\ &= \mathbb{E}_ {x_{1:T} \sim q(x_{1:T}|x_0)}\left[-\log p_{\theta}(x_T) - \sum_{t=2}^T \log \frac{p_{\theta}(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)}\cdot \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} - \log \frac{p_{\theta}(x_0|x_1)}{q(x_1|x_0)}\right] 　　\because † 　　　\\ &= \mathbb{E}_ {x_{1:T} \sim q(x_{1:T}|x_0)}\left[-\log p_{\theta}(x_T) - \sum_{t=2}^T \log \frac{p_{\theta}(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} - \sum_{t=2}^T \log \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} - \log \frac{p_{\theta}(x_0|x_1)}{q(x_1|x_0)}\right] \\ &= \mathbb{E}_ {x_{1:T} \sim q(x_{1:T}|x_0)}\left[-\log p_{\theta}(x_T) - \sum_{t=2}^T \log \frac{p_{\theta}(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} - \log \frac{q(x_1|x_0)}{q(x_T|x_0)} - \log \frac{p_{\theta}(x_0|x_1)}{q(x_1|x_0)}\right] \\ &= \mathbb{E}_ {x_{1:T} \sim q(x_{1:T}|x_0)}\left[-\log \frac{p_{\theta}(x_T)}{q(x_T|x_0)} - \sum_{t=2}^T \log \frac{p_{\theta}(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} - \log p_{\theta}(x_0|x_1)\right] \\ \end{aligned}\] \[\begin{aligned} † \to q(x_t|x_{t-1}) &= q(x_t|x_{t-1}, x_0) 　　\because Markov \ chain \ property \\ &= \frac{q(x_t,x_{t-1},x_0)}{q(x_{t-1},x_0)} 　　\because bayes \ rule \\ &= \frac{q(x_t,x_{t-1},x_0)}{q(x_{t-1},x_0)} \cdot \frac{q(x_t,x_0)}{q(x_t,x_0)} \\ &= q(x_{t-1}|x_t,x_0) \cdot \frac{q(x_t,x_0)}{q(x_{t-1},x_0)} \end{aligned}\]

5번째 줄은 앞서 증명하였듯이 $p_{\theta}$와 $q$가 markov chain임을 이용하여 아래와 같이 표현한 것이다.

\[p_{\theta}(x_{0:T}) = p_{\theta}(x_T)\prod_{t=1}^Tp_{\theta}(x_{t-1}|x_t) 　　　　q(x_{1:T}|x_0) = \prod_ {t=1}^T q(x_ t|x_ {t-1})\]

8번째 줄은 $†$에서 설명한 것 처럼 Markov chain의 성질을 통해 변환한 것이고, 이 과정은 수식 내 $p$와 $q$ distribution이 같은 condition으로부터 같은 target distribution을 가지도록 나타낼 수 있게 해주는 핵심적인 부분이다.

이렇게 loss를 전개해서 최종적으로 나오는 3개의 term을 정리하면 다음과 같다.

\[\mathbb{E}_ q \left[-\log p_{\theta}(x_0)\right] \le \mathbb{E}_ q\left[\underbrace{D_{KL}(q(x_T|x_0) \ || \ p_{\theta}(x_T))}_ {L_T} + \sum_{t>1} \underbrace{D_{KL}(q(x_{t-1}|x_t, x_0) \ || \ p_{\theta}(x_{t-1}|x_t))}_ {L_{t-1}} \underbrace{- \log p_{\theta}(x_0|x_1)}_ {L_0}\right]\]

$L_T$ : VAE의 Regularizaion loss와 대응되는 loss로 $x_T$에 대해 $q$와 $p$의 KL Divergence를 최소화하여 확률분포 차이를 줄인다.
$L_{t-1}$ : VAE에는 없는 새로 추가된 loss term으로 Denoising Process Loss라 부르며 $p$ 와 $q$ 에서 $x_t$가 주어질 때, $x_{t-1}$이 나올 확률분포의 KL Divergence를 최소화하여 확률분포 차이를 줄인다.
$L_0$ : VAE의 Reconstruction Loss와 대응되며, 확률분포 $q$에서 sampling했을 때 $- \log p_{\theta}(x_0 \vert x_1)$의 기댓값을 최소화하여 latent $x_1$에서 input인 $x_0$을 추정하는 모델의 파라미터를 최적화한다.

DDPM Loss

2020년에 발표된 DDPM(Denoising Diffusion Probabilistic Model)은 Diffusion Loss를 아래와 같이 간단하게 재구성하였고, 이렇게 Loss를 간결하게 하면서 성능을 향상시켰다.

\[Loss_{DDPM} = \mathbb{E}_ {x_0,\epsilon} \left[\left|\left|\epsilon - \epsilon_{\theta} \left(\sqrt{\bar{\alpha}_t}x _0 + \sqrt{1-\bar{\alpha}_t}\epsilon, t \right)\right|\right|^2 \right]　, \epsilon \sim \mathcal{N}(0,1)\]

형태를 보면 ground truth인 $\epsilon$과 예측값인 $\epsilon_{\theta}$의 결과값 과의 차이로 이루어져 있음을 알 수 있다. 결과적으로 DDPM Loss는 각 $t$시점의 noise인 $\epsilon$을 모델이 예측하도록 하는 loss이다.

그렇다면 Diffusion Loss가 어떻게 위와 같이 간단하게 정리되는지 알아보면, 우선 Regularizaion term인 $L_T$가 제외된다. Regularizaion term의 목적은 $T$ 시점의 latent variable이 특정 분포(가우시안..)을 따르도록 강제하는 역할인데, 1000번의 step을 걸쳐 noise를 주입해본 결과 $T$ 시점의 latent variable이 isotropic gaussian과 매우 유사함이 밝혀졌기 때문이다. 또한 Reconstruction term인 $L_0$도 제외되는데, 이는 전체적으로 $L_0$의 영향력이 적기 때문이다.

최종적으로 Denoising Process Loss인 $L_{t-1}$만 최소화하면 되는데, 우선 학습 대상에서 분산 $\sigma$는 제외된다. 이유는 noise parameter $\beta_t$를 이미 정하고 학습시키기 때문에, 베타로 분산을 대신하게 된다.

\[\sigma_t^2 \cdot I = \tilde{\beta}_t\cdot I = \text{accumulated noise to point } t\]

Denoising Process term은 gaussian distribution간의 KL divergence이므로 VAE에서처럼 아래와 같이 계산될 수 있다.

\[D_{KL}(p \ || \ q) = \log \frac{\sigma_1}{\sigma_0} + \frac{\sigma_0^2 + (\mu_0 - \mu_1)^2}{2\sigma_1^2} - \frac{1}{2}\]

이때 앞서 설명했듯이 $\sigma$는 학습 파라미터가 없어 상수가 되기 때문에 loss는 $\sigma$를 제외한 $q$와 $p$간의 평균 $\mu$ 차이로, 아래와 같이 정리된다.

\[L_{t-1} = \mathbb{E}_ q \left[\frac{1}{2\sigma_t^2} ||\tilde{\mu}_ t(x_t,x_0) - \mu_{\theta}(x_t,t)||^2 \right] + C\]

위 loss를 계산하기 위해서 $q(x_{t-1} \vert x_t, x_0)$의 평균( $\tilde{\mu}_ t(x_t,x_0)$ )과 $p_{\theta}(x_{t-1} \vert x_t)$의 평균( $\mu_{\theta}(x_t,t)$ )을 구하면 된다.

Calculate the mean of $q$

평균을 구하기 앞서 $q(x_{t-1} \vert x_t,x_0)$를 베이즈 정리를 이용해 아래와 같이 표현할 수 있다.

\[q(x_{t-1}|x_t,x_0) = q(x_t|x_{t-1},x_0) \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\]

이를 계산하기 위해선 $q(x_t \vert x_0)$와 $q(x_t \vert x_{t-1})$각각의 분포를 tractable한 가우시안 형태로 알아야 한다.
앞서 Diffusion Process에서 보았듯이 $q(x_t \vert x_{t-1})$를 Reparameterization Trick으로 표현하면 다음과 같다.

\[x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1}\] \[\alpha_t := 1-\beta_t \ and \ \bar{\alpha} := \prod_{s=1}^t \alpha_s\]

기호를 위와 같이 알파로 재정의하면 $x_t$는 아래와 같이 정의된다.

\[\begin{aligned} x_t &= \sqrt{\alpha_t}x_{t-1} + \sqrt{1-\alpha_t}\epsilon_{t-1}　　　　　　　\ 　　\ 　　　　;\epsilon_{t-1}, \epsilon_{t-2},... \sim \mathcal{N}(0,1) \\ &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon_{t-2}) + \sqrt{1-\alpha_t}\epsilon_{t-1} 　　; x_{t-1} = \sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon_{t-2} \\ &= \sqrt{\alpha_t \alpha_{t-1}}x_{t-2} + \sqrt{\alpha_t(1-\alpha_{t-1})}\epsilon_{t-2} + \sqrt{1-\alpha_t}\epsilon_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_t \alpha_ {t-1}}\bar{\epsilon}_ {t-2}　　\ 　　　　 \ 　　　;\bar{\epsilon}_ {t-2} \ \text{merges two Gaussians}　(*) \\ &\cdots \\ &= \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon \\ \end{aligned}\]

(*) Recall that when we merge two Gaussians with different variance, $\mathcal{N}(0, \sigma_1^2I)$ and $\mathcal{N}(0, \sigma_2^2I)$, the new distribution is $\mathcal{N}(0, (\sigma_1^2+\sigma_2^2)I)$.
Usually, we can afford a larger update step when the sample gets noisier, so $\beta_1 < \beta_2 < \cdots < \beta_T$ and therefore $\bar{\alpha_1} > \cdots > \bar{\alpha_T}$.

결과적으로 $q(x_t \vert x_0)$는 아래와 같이 표현된다.

\[q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I)\]

이제 $q(x_t \vert x_0)$와 $q(x_t \vert x_{t-1})$ 분포를 tractable한 가우시안 형태로 아래와 같이 표현할 수 있다.

\[\begin{aligned} &q(x_t|x_0) \sim \mathcal{N}(\sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)I) \\ &q(x _t|x _{t-1}) \sim \mathcal{N}(\sqrt{1-\beta_t}x _{t-1}, \beta_tI) \end{aligned}\]

이를 이용하여 $q(x_{t-1} \vert x_t,x_0)$를 계산하면 다음과 같다.

\[\begin{aligned} q(x_{t-1}|x_t,x_0) &= q(x_t|x_{t-1},x_0) \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &\propto \exp\left(-\frac{1}{2}\left(\frac{(x_t - \sqrt{\alpha_t}x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_ {t-1}}x_0)^2}{1 - \bar{\alpha}_ {t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_ t}x_{0})^2}{1 - \bar{\alpha}_t}\right) \right) \\ &= \exp\left(-\frac{1}{2}\left(\frac{x _t^2 - 2\sqrt{\alpha _t}x _t x _{t-1} + \alpha _t x _{t-1}^2}{\beta _t} + \frac{x _{t-1}^2 - 2\sqrt{\bar{\alpha} _{t-1}}x _0 x _{t-1} + \bar{\alpha} _{t-1} x _0^2}{1 - \bar{\alpha} _{t-1}} - \frac{(x _t - \sqrt{\bar{\alpha} _t}x _{0})^2}{1 - \bar{\alpha} _t} \right) \right) \\ &= \exp\left(-\frac{1}{2}\left(\left(\frac{\alpha _t}{\beta _t} + \frac{1}{1 - \bar{\alpha} _{t-1}}\right)x _{t-1}^2 - \left(\frac{2\sqrt{\alpha _t}}{\beta _t}x _t + \frac{2\sqrt{\bar{\alpha} _{t-1}}}{1 - \bar{\alpha} _{t-1}}x _0 \right)x _{t-1} + C(x _t, x _0) \right) \right) \end{aligned}\]

2번째 줄의 비례식은 가우시안 분포의 확률 밀도 함수(probability density function)에 의해 성립한다.

\[f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \propto e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\]

4번째 줄의 $C(x _t, x _0)$는 $x _{t-1}$과 관련이 없기 때문에 상수처리된다.

이제 최종적으로 나온 exponential 내부를 가우시안 pdf 형태인 $-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2$의 형태로 표현하면 평균과 분산은 다음과 같이 정리된다.

\[\begin{aligned} \tilde{\mu}_ t(x_ t,x_ 0) &= \frac{\left(\frac{\sqrt{\alpha _t}}{\beta _t}x _t + \frac{\sqrt{\bar{\alpha} _{t-1}}}{1 - \bar{\alpha} _{t-1}}x _0 \right)}{\left(\frac{\alpha _t}{\beta _t} + \frac{1}{1-\bar{\alpha} _{t-1}}\right)} \\ &= \left(\frac{\sqrt{\alpha _t}}{\beta _t}x _t + \frac{\sqrt{\bar{\alpha} _{t-1}}}{1 - \bar{\alpha} _{t-1}}x _0 \right) \cdot \frac{1-\bar{\alpha} _{t-1}}{1-\bar{\alpha} _t} \cdot \beta _t \\ &= \frac{\sqrt{\alpha _t}(1 - \bar{\alpha} _{t-1})}{1 - \bar{\alpha} _t} x _t + \frac{\sqrt{\bar{\alpha} _{t-1}} \beta _t}{1 - \bar{\alpha} _t} x _0 \end{aligned}\] \[\tilde{\beta_t} = \frac{1}{\left(\frac{\alpha _t}{\beta _t} + \frac{1}{1-\bar{\alpha} _{t-1}}\right)} = \frac{1}{\left( \frac{\alpha _t - \bar{\alpha} _t + \beta_t}{\beta_t(1-\bar{\alpha} _{t-1})} \right)} = \frac{1-\bar{\alpha} _{t-1}}{1-\bar{\alpha} _t} \cdot \beta _t\]

추가적으로 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon$ 이므로 $x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1 - \bar{\alpha}_t}\epsilon _t)$이다. 이를 $\tilde{\mu}$에 적용하면 아래와 같이 된다.

\[\begin{aligned} \tilde{\mu}_ t &= \frac{\sqrt{\alpha _t}(1 - \bar{\alpha} _{t-1})}{1 - \bar{\alpha} _t} x _t + \frac{\sqrt{\bar{\alpha} _{t-1}} \beta _t}{1 - \bar{\alpha} _t} \cdot \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1 - \bar{\alpha}_t}\epsilon _t) \\ &= \frac{1}{\sqrt{\alpha _t}} \left(x _t - \frac{1 - \alpha _t}{\sqrt{1 - \bar{\alpha}_t}}\epsilon _t \right) \end{aligned}\]

정리하면 다음과 같다.

\[\tilde{\mu}_ t = \frac{1}{\sqrt{\alpha _t}} \left(x _t(x _0, \epsilon) - \frac{1 - \alpha _t}{\sqrt{1 - \bar{\alpha}_t}}\epsilon _t \right),　\tilde{\beta_t} = \frac{1-\bar{\alpha} _{t-1}}{1-\bar{\alpha} _t} \cdot \beta _t\]

Calculate the mean of $p_{\theta}$

지금까지의 내용으로 $Loss$를 표현하면 다음과 같다.

\[L_ {t-1} = \mathbb{E} _q \left[\frac{1}{2\sigma _t^2} \left|\left|\frac{1}{\sqrt{\alpha _t}} \left(x _t(x _0, \epsilon) - \frac{1 - \alpha _t}{\sqrt{1 - \bar{\alpha} _t}}\epsilon _t \right) - \mu _{\theta}(x_t(x _0,\epsilon),t)\right|\right|^2 \right]\]

여기서 네트워크는 굳이 $x_t(x _0,\epsilon)$를 학습할 필요가 없는데, 그 이유는 time step- $t$에서 이미 input으로 $x_t$가 주어지고, $x _{t-1}$을 만들기 위한 확률분포 예측과정이므로 Diffusion Process에서 stochastic(확률론적)으로 더해졌던 epsilon($\epsilon$)부분만 예측하면 된다. 따라서 epsilon만 학습하도록 $\mu _{\theta}(x _t, t)$를 정의해주면 아래와 같다.

\[\mu _{\theta}(x _t, t) = \frac{1}{\sqrt{\alpha _t}} \left(x _t - \frac{1 - \alpha _t}{\sqrt{1 - \bar{\alpha} _t}}\epsilon _{\theta}(x _t, t) \right)\]

DDPM Loss

앞서 설명했듯이 $Loss_{DDPM}$는 아래 수식을 계산하면 된다고 했다.

\[L_{t-1} = \mathbb{E}_ q \left[\frac{1}{2\sigma_t^2} ||\tilde{\mu}_ t(x_t,x_0) - \mu_{\theta}(x_t,t)||^2 \right] + C\]

이는 확률분포 $q$로 sampling했을 때의 기댓값 식이고, $x_0$와 가우시안 분포($\epsilon$)로 sampling하고, 상수 $C$를 제거하면 $Loss_{DDPM}$이 다음과 같이 정리된다.

\[\begin{aligned} Loss_ {DDPM} &= \mathbb{E}_ {x _ 0,\epsilon} \left[\frac{1}{2\sigma_ t^2} ||\tilde{\mu}_ t(x_t,x_0) - \mu_{\theta}(x_t,t)||^2 \right] \\ &= \mathbb{E} _{x _0,\epsilon} \left[\frac{1}{2\sigma _t^2} \left|\left| \frac{1}{\sqrt{\alpha _t}} \left(x _t - \frac{1 - \alpha _t}{\sqrt{1 - \bar{\alpha} _t}}\epsilon _t \right) - \frac{1}{\sqrt{\alpha _t}} \left(x _t - \frac{1 - \alpha _t}{\sqrt{1 - \bar{\alpha} _t}}\epsilon _{\theta}(x _t, t) \right) \right|\right|^2 \right] \\ &= \mathbb{E} _{x _0,\epsilon}\left[\frac{\beta _t^2}{2\sigma _t^2 \alpha _t (1 - \bar{\alpha} _t)} \left|\left|\epsilon - \epsilon _{\theta}(\sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\epsilon, t) \right|\right|^2 \right] \end{aligned}\]

논문에서는 coefficient를 제거하여 loss를 계산하는 것이 성능이 더 좋았다고 한다.

\[Loss_{DDPM} = \mathbb{E}_ {x_0,\epsilon} \left[\left|\left|\epsilon - \epsilon_{\theta} \left(\sqrt{\bar{\alpha}_t}x _0 + \sqrt{1-\bar{\alpha}_t}\epsilon, t \right)\right|\right|^2 \right]　, \epsilon \sim \mathcal{N}(0,1)\]

Reference

Web Link

PRML : http://norman3.github.io/prml/docs/chapter01/0
Entropy : https://hyunw.kim/blog/2017/10/14/Entropy.html
Bayes Rule : https://angeloyeo.github.io/2020/01/09/Bayes_rule.html#google_vignette
MLE, MAP : https://niceguy1575.medium.com/mle%EC%99%80-map%EC%9D%98-%EC%B0%A8%EC%9D%B4-7d2cc0bee9c
Mahalanobis distance : https://angeloyeo.github.io/2022/09/28/Mahalanobis_distance.html
KL between 2 Gaussian : https://mr-easy.github.io/2020-04-16-kl-divergence-between-2-gaussian-distributions/
Trace Trick : http://en.wikipedia.org/wiki/Estimation_of_covariance_matrices#The_trace_of_a_1_.C3.97_1_matrix
VAE : https://youtu.be/o_peo6U7IRM?si=aD8yhUPwGtfP9y7c
　 　 https://youtu.be/rNh2CrTFpm4?si=jb_R-gFrYzo9XQ5b
　 　 https://avandekleut.github.io/vae/
　 　 https://enfow.github.io/paper-review/generative-model/2020/03/28/VAE-auto_encoding_variational_bayes/
DDPM : https://youtu.be/H45lF4sUgiE?si=vmEdXqhlLF_zesjO
　 　 　https://youtu.be/_JQSMhqXw-4?si=Iifr0t5xFzDSYKky
　 　 　https://youtu.be/uFoGaIVHfoE?si=yoj18GZsi41nW84W
　 　 　https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
　 　 　https://xoft.tistory.com/33
　 　 　https://developers-shack.tistory.com/8
　 　 　https://junia3.github.io/blog/DDPMproof
Stable Diffusion : https://github.com/hkproj/pytorch-stable-diffusion/tree/main
　  　　　 　  　 https://youtu.be/ZBKpAp_6TGI?si=8Ytizix8c5BFRQhr

Paper

Tutorial on Variational Autoencoders : https://arxiv.org/pdf/1606.05908.pdf
VAE : https://arxiv.org/pdf/1312.6114.pdf
DDPM : https://arxiv.org/pdf/2006.11239.pdf