Elliptic Curve

Weierstrass Curve

Elliptic Curve

An elliptic curve is a graph of a curve showing a set of $x$ and $y$ that satisfy the equation below.

\[\lbrace (x, y) ∈ ℝ^2 \vert y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0 \rbrace ∪ \lbrace0\rbrace\]

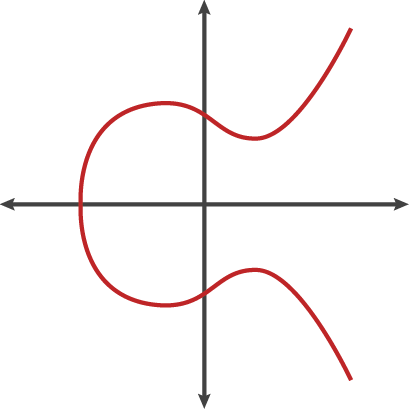
The shape of the above elliptic curve is called the Weierstrass elliptic curve, and there are other types of elliptic curves such as Montgomery, Edwards, Jacobi, and Hessian.

Elliptic Curve over Group

1. Elements : Points of an curve
2. Identity element : Point at infinity or ideal point -> 0
3. Inverse element : Point symmentric about $x$ - axis
4. Addition : Given aligned three points $P$, $Q$, $R$ -> $P + Q + R = 0$ (abelian group)

Geometric Addition

$P + Q + R = 0, P + Q = -R$

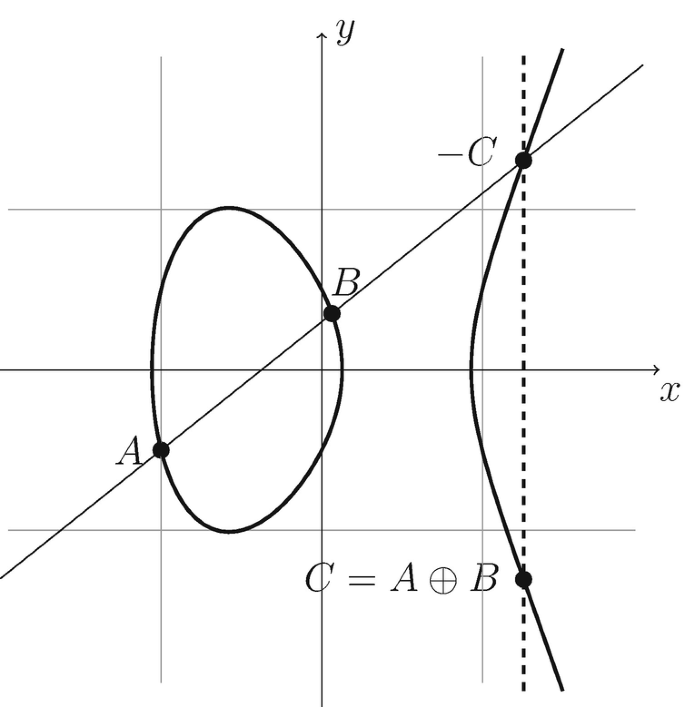
case

1. $P = 0$ $or$ $Q = 0$
   -> Identity element
   -> $P + 0 = P$ $or$ $0 + Q = Q$

2. $P = -Q$
   -> Inverse element
   -> $-Q + Q = 0$

3. $P = Q$ $or$ $P≠Q$ $but$ $no$ $R$
   -> Tangency

Algebraic Addition

\[P + 0 = P,\ -Q + Q = 0\] \[\begin{align} x_R = λ^2-x_P-x_Q \\ y_R = λ(x_P-x_R)-y_P \end{align}\] \[where \ λ = \begin{cases} \frac{y_P - y_Q} {x_P - x_Q} &if \ (x_P, y_P) \neq (x_Q, \pm y_Q), \\ \frac{3x_P^2 + a} {2y_P} &if \ (x_P, y_P)=(x_Q, y_Q). \end{cases}\]

(Proof) $if(P == Q)$ -> $tangency
$y^2 = x^3 + ax + b$
$f(x)^2 = x^3 + ax + b$
$f(x)^2 - x^3 - ax - b = 0$
$2f(x)f’(x) -3x^2 -a = 0$

$λ = \frac{3x^2 + a} {2y}$

$λ = \frac{y_P - y_Q} {x_P - x_Q}$
$y - y_P = λ(x - x_P)$
∴ $y_R = λ(x_P - x_R) - y_P \because P+Q=-R$

$y^2 = x^3 + ax + b$
$y = λ(x - x_P) + y_P$
$x^3 + ax + b = \lbrace y_P + λ(x - x_P) \rbrace^2$
$x^3 -λ^2x^2 … + b = 0$
$using$ $Viète’s$ $theorem$ $on$ $cubic$ $equation$
$x_P + x_Q + x_R = λ^2$
∴ $x_R = λ^2 - x_P - x_Q$

Double and Add Algorithm

in order to efficiently compute $nP$ from the known values $n$ and $P$ we use Double and Add Algorithm.

We first write $n$ in binary form as

\[n = n_0 + n_1·2 + n_2·4 + n_3·8 + ··· + n_r·2^n \ with \ n_0, n_1, ···, n_r ∈ {0, 1}\]

(We also assume that $n_r = 1$.) Next we compute the following quantities:

\[Q_0 = P, Q_1 = 2Q_0, Q_2 = 2Q_1, ..., Q_r = 2Q_{r-1}\]

Notice that $Q_i$ is simply twice the previous $Q_{i−1}$ so

\[Q_i = 2^iP\]

These points are referred to as 2-power multiples of $P$, and computing them requires r doublings. Finally, we compute $nP$ using at most $r$ additional additions,

\[nP = n_0Q_0 + n_1Q_1 + n_2Q_2 + ··· + n_rQ_r\]

Elliptic Curves Over Galois Field

GF stands for Finite Field, a sieve with finite elements.
It exists in infinitely finite places in x, y and coordinate systems, using Modular to create GFs.

$E : y^2 = x^3 + x$ $over$ $Z_{23}$

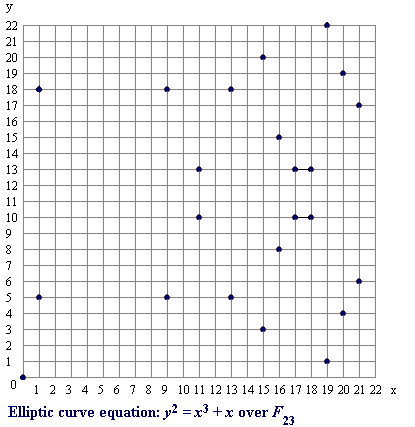
The figure above shows all the coordinates that exist on the GF when p is 23.
$If$ $x = 11,$
$y^2mod$ $23 ≡ (1331+11)mod$ $23 ≡ 1342mod$ $23 ≡ 8$
to find a value of $y$ that satisfies
$y^2mod$ $23 ≡ 8$
We need to get the expression above, and what can be the value of y is 10 and 13.

At this time, if the p in the field of GF becomes larger, it becomes difficult to find y, which can be used to perform encryption.

Elliptic curve encryption algorithm

G: constructor, any point on the elliptic curve
x : Private key, prime less than P, generated by random number generator
Q: Public key, calculation from private key

When point $P=(x, y)$ is located on an elliptical curve, you can define the following equation for two points $P$, $Q$ and any integer $x$.
$Q = xG$

At this point, the elliptic curve discrete algebra problem is to find the value of $x$, and the public key $Q$ is $Q = xG = G + G + … + G$ is the value of adding G x times.

In the $Q = xG$ formula, it is easy to obtain $Q$ using $x$ and $G$, but it is difficult to obtain $x$ through known $G$ values and $Q$ values.

This is called the Elliptic Curve Discrete Logarithm Problem (ECDLP), and because of this property, it is used as a public key cryptography technology.

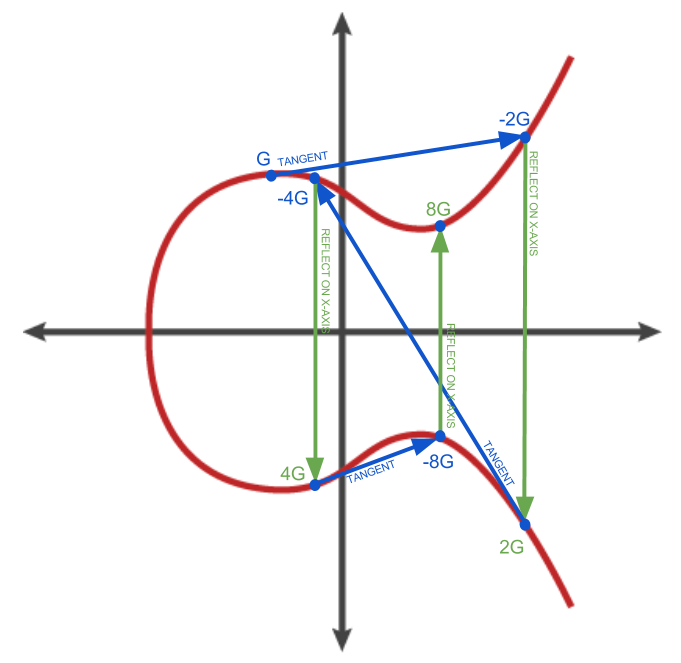
The figure above is a geometric schematic of the computational process of $xG$.

Looking at the 2P doubling of P in the addition operation of the elliptic curve encryption algorithm (ECC), $2G = G + G$ is the point where the tangent at point $G$ meets the elliptic curve symmetrically on the x-axis. $4G = 2G + 2G$ is the x-axis symmetrical point of the point that meets the elliptical curve by drawing a tangent similarly to the point corresponding to $2G$.

Constant multiplication of G can do this repeatedly.

The elliptic curve is one of the mathematical methods of performing a public key cryptographic system, which can be used to implement RSA, ElGamal, and Diffie-Hellman.

Let’s use the example to learn how to generate keys using elliptic curve algorithms.

The given expression is shown below.

$E: y^2 = x^3 + x + 6$ $over$ $Z_{11}$
$G(α) = (2,7)$
$2α = (x_2,y_2)$

$λ = \frac{3x_1^2 \ + \ a}{2y_1} = \frac{3(2)^2 \ + \ 1}{2 \ * \ 7} = \frac{13}{14} = 2 \ * \ 3^{-1} = 2 * 4 = 8 \mod{11}$

$x_ 2 = λ^2 - 2x_ 1 = (8)^2 - 2*(2) = 5 \mod{11}$

$y_ 2 = (x_ 1 - x_ 2)λ - y_ 1 = (2 - 5)*8 - 7 = 2 \mod{11}$

$2α = (5, 2)$

You can use this method to obtain $α, 2α, …, kα$.

$Private$ $key(x)*α=Public$ $key(Q)$

Edwards curve

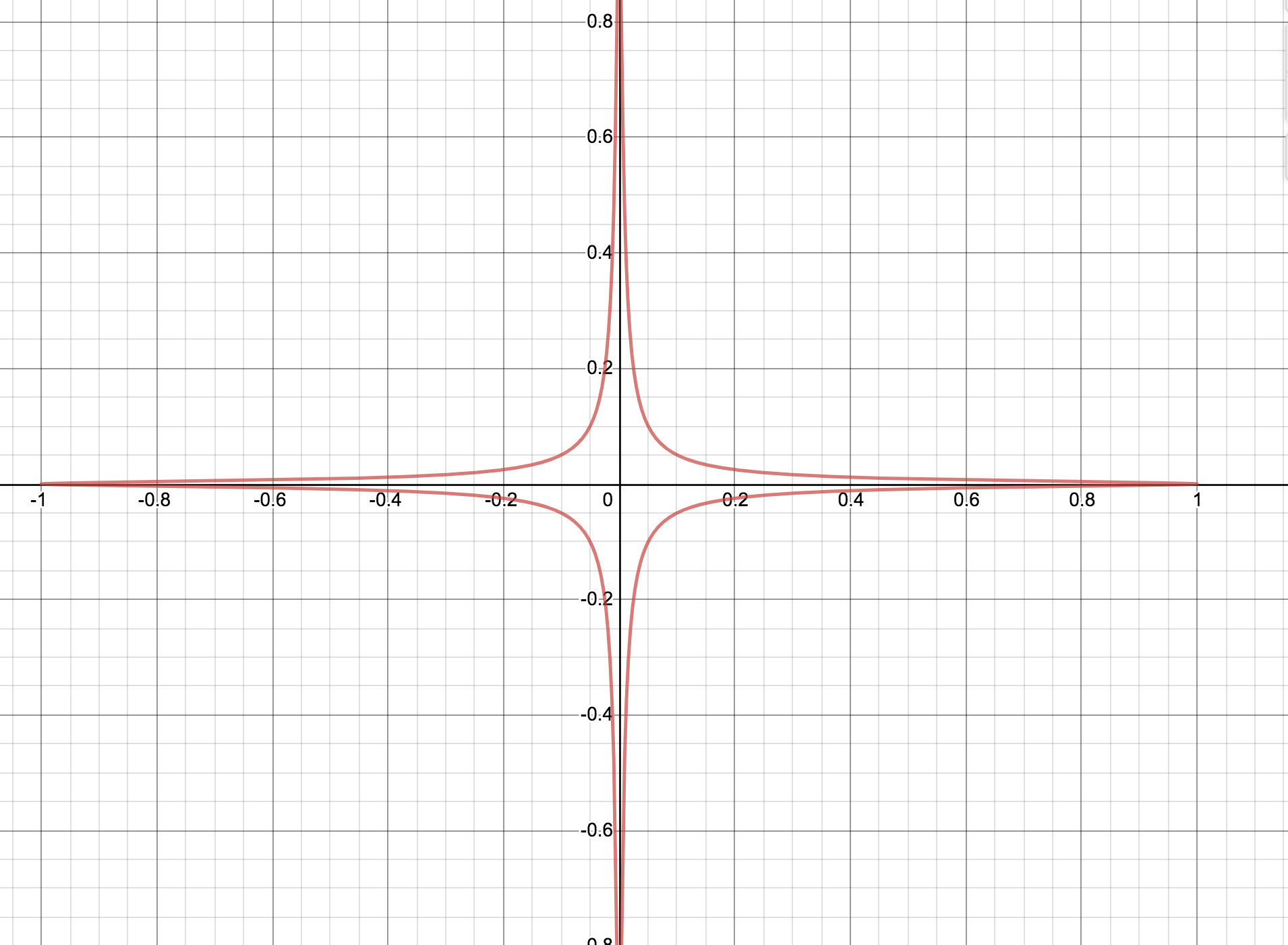
The equation of an Edwards curve over a field K which does not have characteristic 2 is:

\[x^2 + y^2 = 1 + dx^2y^2 \ where \ c, d ∈ K \ with \ cd(1 − c^4·d) ≠ 0\]

Edwards addition law

the sum of the points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula

\[(x_1, y_1) + (x_2, y_2) = \left( \frac{x_1y_2 + x_2y_1}{1 + dx_1x_2y_1y_2}, \frac{y_1y_2 - x_1x_2}{1 - dx_1x_2y_1y_2}\right)\]

The opposite of any point $(x, y)$ is $(-x, y)$. The point $(0, -1)$ has order 2, and the points $(±1, 0)$ have order 4. In particular, an Edwards curve always has a point of order 4 with coordinates in $K$.

One of the attractive feature of the Edwards Addition law is that it is strongly unified i.e. it can also be used to double a point, simplifying protection against side-channel attack. The addition formula above is faster than other unified formulas and has the strong property of completeness

An analogue on the circle

To understand better the concept of “addition” of points on a curve, a nice example is given by the classical circle group:
take the circle of radius 1

\[x^2 + y^2 = 1\]

and consider two points $P_1=(x_1,y_1), P_2=(x_2,y_2)$ on it. Let $α_1$ and $α_2$ be the angles such that:

\[P_1 = (x_1, y_1) = (\sin α_1, \cos α_1)\] \[P_2 = (x_2, y_2) = (\sin α_2, \cos α_2)\]

The sum of $P_1$ and $P_2$ is, thus, given by the sum of “their angles”. That is, the point $P_3=P_1+P_2$ is a point on the circle with coordinates $(x_3,y_3)$, where:

\[x_3 = \sin (α_1 + α_2) = \sin α_1 \cos α_2 + \cos α_1 \sin α_2 = x_1y_2 + x_2y_1\] \[y_3 = \cos (α_1 + α_2) = \cos α_1 \cos α_2 - \sin α_1 \sin α_2 = y_1y_2 - x_1x_2\]

In this way, the addition formula for points on the circle of radius 1 is:

\[(x_1, y_1) + (x_2, y_2) = (x_1y_2 + x_2y_1, y_1y_2 - x_1x_2)\]

Doubling

Doubling can be performed with exactly the same formula as addition. Doubling refers to the case in which the inputs $(x_1, y_1)$ and $(x_2, y_2)$ are equal.

Doubling a point $P = (x, y):$

\[\begin{aligned} (x, y) + (x, y) &= \left( \frac{2xy}{1 + dx^2y^2}, \frac{y^2 - x^2}{1 - dx^2y^2}\right) \\ &= \left( \frac{2xy}{x^2 + y^2}, \frac{y^2 - x^2}{2 - x^2 - y^2}\right) \end{aligned}\]

The denominators were simplified based on the curve equation $x^2 + y^2 = 1 + dx^2y^2$. Further speedup is achieved by computing $2xy$ as $(x+y)^2 - x^2 - y^2$. This reduces the cost of doubling in homomorphic coordinates to $3M + 4S + 3C + 6a$. Here $M$ is field multiplications, $S$ is field squarings, $D$ is the cost of multiplying by the curve parameter $d$, and $a$ is field addition.

Edwards -> Montgomery -> Weierstrass

Edwards, Montgomery, and Weierstrass are Equivalences, so Curve transformation and Points mapping are possible through the relationship below.

1. Edwards -> Montgomery
   When the form of Edwards curves is $\mathcal{E}_{e}^{a, d} : ax^2 + y^2 = 1 + dx^2y^2$ and the form of Montgomery curves is $\mathcal{E}_m^{A, B}: By^2 = x^3 + Ax^2 + x$, $\mathcal{E}_e^{a, d}$ is converted to Montgomery curves $\mathcal{E}_m^{2(a + d)/(a - d), 4/(a - d)}$, and the Point map is $(x, y) \mapsto \left(\frac{1 + y}{1 - y}, \frac{1 + y}{x - xy}\right)$.

2. Montgomery -> Weierstrass
   When the form of Montgomery curves is $\mathcal{E}_ m^{A, B}: By^2 = x^3 + Ax^2 + x$ and the form of Weierstrass curves is $\mathcal{E}_{w}^{a, b} : y^2 = x^3 + ax + b$, $\mathcal{E}_m^{A, B}$ is converted to Weierstrass curve $\mathcal{E}_w^{1/B^2-A^2/3B^2,A(2A^2 - 9)/27B^3}$, and the Point map is $(x, y) \mapsto \left(x+\frac{A}{3}, \frac{y}{B} \right)$.

ECDLP (Elliptic Curve Discrete Logarithm Problem)

the elliptic curve discrete logarithm problem is: given points $P$ and $Q$ in the group, find a number that $Pk = Q$ k is called the discrete logarithm of $Q$ to the base $P$. When the elliptic curve group is described using additive notation, the elliptic curve discrete logarithm problem is: given points $P$ and $Q$ in the group, find a number $k$ such that $Pk = Q$

It is of cryptographic interest because its apparent intractability is the basis for the security of elliptic curve cryptography.

Anomalous Elliptic Curve

Anomalous elliptic curve has a curve of defined above $F_p$, it means a curve whose order is $p$. Defining an elliptical curve determines the number of points that can exist on that curve, which is called an order.

Let’s say that the order of the curve is the composite number $n$ and the factorization is possible, and the result is $n=p_1p_2..p_k$. Then we can split the entire group of points into subgroups of $p_i$ points for each prime factor $p_i$. The size of this subgroup is smaller than $n$, making it easier to attack, and the results for each subgroup can be combined into one. Therefore, if the curve defined for $F_p$ of prime $p$ has $order \ p$, it is considered relatively less vulnerable to attack because it is equally prime.

One where $𝐸(𝐹𝑝)$ which mean The order does not have sufficiently large prime subgroups and is subject to the Pohlig-Hellman attack, and another where $𝐸(𝐹𝑝) = 𝑝$ allowing an Smart’s Attack

ECDH(Elliptic Curve Diffie Hellman)

ECDH is a method of applying Diffie–Hellman key exchange to the Elliptic Curve.

The ECDH algorithm is as follows:

1. Alice and Bob each create a (public key, private key) pair. Let’s say Alice and Bob’s key pair is $(d_A, H_A), (d_B, H_B)$ and b, respectively. $H_A = d_AG, H_B = d_BG$.
2. Alice and Bob exchange each other’s public keys. $(H_A, H_B)$
3. Alice calculates $S=d_AH_B$, Bob calculates $S=d_BH_A$.
   The formula $S=d_AH_B=d_A(d_BG)=d_B(d_AG)=d_BH_A$ calculated by Alice and Bob are the same. Alice and Bob share a secret key.

ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA is a cryptographic algorithm that incorporates elliptic curve ciphers into electronic signatures. In Bitcoin and Ethereum, ECDSA is being used as SECP256K1. The private key and the public key have a pair.

The elliptic curve function used in Ethereum and Bitcoin is SECP256K1, which is as follows.

\[y^2 = x^3 + 7\]

SECP256K1 is an elliptical curve with $a$ of $0$ and $b$ of $7$ and a reference point $G$ of (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8).

p : 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a : 0x0000000000000000000000000000000000000000000000000000000000000000
b : 0x0000000000000000000000000000000000000000000000000000000000000007
G : (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
n : 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h : 0x1

https://neuromancer.sk/std/

1. Private Key

A Private Key is one of the integers in $1$ ~ $n-1$.

Here, n is defined as $1.157920892373162e+77$ under the SECP256K1 elliptic curve, expressed in hexadecimal as FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFEBAEDCE6AF48A03BFD25E8CD0364141.

In other words, the private key is to obtain a value between 1 and FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAEDCE6AF48A03BBFD25E8CD0364141.

Outside of this range, Ethereum sends an error saying it is an invalid private key.

2. Signature $r$

Choose $1$ to $n - 1$ integers randomly, as in obtaining a Private Key. While the private key is used only once selected, this value must be obtained each time a transaction is sent. This value becomes $k$.

1. Generate an arbitrary value $k$ (20 bytes). Calculate $P = k$ x $G$ using the multiplication of points.
2. The $x$ value of the point $P$ represents $r$. (20 bytes)

3. Signature $s$

\[s = k^{-1}(z + r * Private \ Key)\mod{n}\]

z : Value containing transaction information(hash)
At this time, if the calculation value is $0$, the random number $K$ must be newly generated and recalculated.

When transmitting a transaction, you can send a transaction containing the contents and signatures $r$ and $s$.

4. Verification

\[U1 = z * w \mod{n}\] \[U2 = r * w \mod{n}\] \[w = s^{-1} \mod{n}\] \[U1 * G + U2 * Private \ Key\]

The public key is the recovery key, and Ethereum uses an integer 27 or 28, not a signature value.

The above equation is an operation of the elliptic curve, and the result is a point on the elliptic curve. And you can compare whether the $x-coordinate$ of that point is the same as the signature $r$ that I received.

5. Public Key

The public key can be sent by the person who sends the transaction, but it does not do so in Ethereum. The original public key can be obtained using the recovery key. In Ethereum, this recovery key is promised at the value of 27 or 28, so you can extract the sender’s public key using the recovery key only with a signature.

In summary, public keys can be extracted from signatures $v$, $r$, and $s$ in the transaction. In solidity, there is a function called ecrecover.

The public key can be obtained from the private key. You can multiply the secret key by the reference point $G$ set in Ethereum.

As mentioned above, the secret key is a simple integer, so it is only a constant, and the point $G$ is a point on the elliptical curve, so the public key is also a point on the elliptical curve.

\[Public \ Key = Private \ Key * G\]

6. Address

The address can be obtained from the public key. The address is hexadecimal and the last 20 bytes of the public key’s Keccak-256 hash are obtained.

function publicKeyToAddress(pubKey: Buffer): Buffer {
  return keccak256(pubKey).slice(-20)
}

Reference

ECC : https://developer-mac.tistory.com/83 , https://www.youtube.com/watch?v=_GOmrsCbNss ,
　　  https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
ECDLP : https://rbtree.blog/posts/2020-05-19-anomalous-elliptic-curve/
　　　  https://wstein.org/edu/2010/414/projects/novotney.pdf
　　　  https://github.com/jvdsn/crypto-attacks/blob/master/attacks/ecc/smart_attack.py
ECDH : https://velog.io/@dohoon8/Cryptography-4.-ECDH%EC%99%80-ECDSA%EC%97%90-%EB%8C%80%ED%95%98%EC%97%AC-pgbr3e5a
ECDSA : https://www.jongho.dev/blockchain/ethereum-sign-and-ecdsa/
Edwards curve : https://en.wikipedia.org/wiki/Edwards_curve
Elliptic Curve Models & Curve Attacks(*) : https://eprint.iacr.org/2015/1233.pdf